KD 1.6 PERSAMAAN GARIS LURUS

Persamaan Garis Lurus

Suatu garis dapat dikenali melalui persamaannya dengan melihat gradien dan salah satu titik yang dilaluinya. Misalnya, garis y = mx + c dengan gradien m melalui titik (x₁, y₁), berarti y₁ =mx₁ + c ⇔ c = y₁ – mx₁ .

Ayo, substitusi nilai c pada y = mx + c sehingga didapat:

y = mx + y₁ – mx₁

y – y₁ = m(x – x₁) …. (*)

Persamaan (*) dapat pula diperoleh secara geometri.

Coba perhatikan garis y = mx + c yang melalui titik A(x₁, y₁) dan bergradien m.

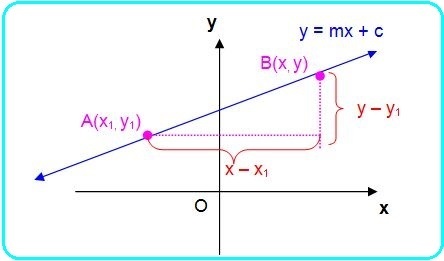
Jika titik B(x, y) adalah titik sebarang pada garis y = mx + c maka:

m=y−y1x−x1 ⇔ y – y₁ = m(x – x₁)

Contoh

 Tentukan persamaan garis g yang melalui titik (4, 6) dan bergradien 3.

Tentukan pula persamaan garis k yang melalui titik (-2, 3) dan sejajar garis g.

Jawab:

Persamaan garis yang melalui titik (4, 6) dan bergradien 3 adalah sebagai berikut.

y – y₁ = m(x – x₁)

⇔ y – 6 = 3(x – 4)

⇔ y = 3x – 12 + 6

⇔ y = 3x – 6

Jadi, persamaan garis g yang melalui titik (4, 6) dan bergradien 3 adalah y = 3x – 6.

Pada bagian sebelumnya, kamu telah mengetahui bahwa dua garis yang sejajar memiliki gradien yang sama. Oleh karena garis k//g, maka mk = mg. Dengan demikian, mk = 3. Jadi, garis k adalah garis yang melalui titik (-2, 3) dan bergradien 3 sehingga persamaannya adalah sebagai berikut.

y – y₁ = m(x – x₁)

⇔y – 3 = 3(x – (-2))

⇔ y = 3x + 6 + 3

⇔ y = 3x + 9

Jadi, persamaan garis yang melalui titik (-2, 3) dan sejajar garis g adalah y = 3x + 9.