Pertidaksamaan irasional yaitu pertidaksamaan yang variabelnya terletak di bawah tanda akar.
Ada dua bentuk umum pertidaksamaan bentuk akar, yaitu:
Ada dua bentuk umum pertidaksamaan bentuk akar, yaitu:
1)
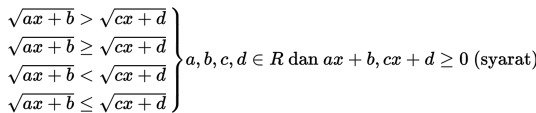
2)
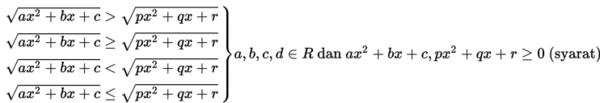
Dalam menyelesaikan pertidaksamaan irrasional terdapat syarat tambahan selain ketentuan umum, yaitu sebagai berikut.
a. Bentuk yang ada di bawah tanda akar ≥ 0.
Misalnya: pada √(x – 2), harus berlaku x – 2 ≥ 0.
b. Bilangan hasil penarikan akar adalah 0.
Misalnya: pada √(x – 2), harus berlaku x – 2 ≥ 0.
b. Bilangan hasil penarikan akar adalah 0.
Mari kita mencermati beberapa contoh soal berikut ini.
Contoh 1:
Tentukanlah himpunan penyelesaian dari pertidaksamaan dari

Penyelesaian:
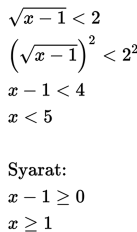
Jadi, himpunan penyelesaian adalah
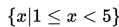
Contoh 2:
Tentukanlah himpunan penyelesaian dari pertidaksamaan dari
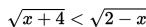
Penyelesaian:
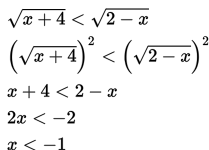

Syarat:
a. x + 4 ≥ 0
x ≥ -4
a. x + 4 ≥ 0
x ≥ -4

b. 2 – x ≥ 0
-x ≥ - 2
x ≤ 2
-x ≥ - 2
x ≤ 2
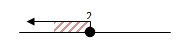
Irisan dari x < -1, x ≥ -4, dan x ≤ 2 merupakan himpunan penyelesaian pertidaksamaan tersebut.
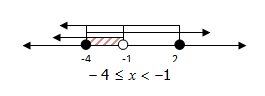
Jadi, himpunan penyelesaian adalah
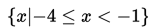
Contoh 3:
Selesaikan pertidaksamaan
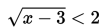
Penyelesaian:
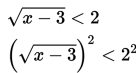
x – 3 < 4
x < 7
x < 7
Syarat:
x – 3 ≥ 0
x ≥ 3
x – 3 ≥ 0
x ≥ 3
Jadi, himpunan penyelesaian adalah
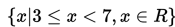
Contoh 4:
Selesaikan pertidaksamaan
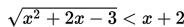
Penyelesaian:
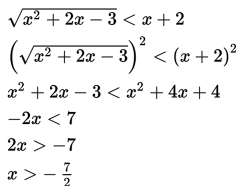
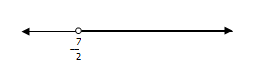
Syarat:
a. x2 + 2x – 3 ≥ 0
(x + 3)(x – 1) ≥ 0
x ≤ -3 atau x ≥ 1
(x + 3)(x – 1) ≥ 0
x ≤ -3 atau x ≥ 1

b. x + 2 > 0
x > -2
x > -2
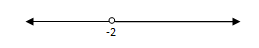
Jadi, himpunan penyelesaian adalah
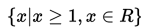
No comments:
Post a Comment