Sebelum kalian mempelajari topik ini, mari kita ingat kembali konsep turunan menggunakan limit fungsi berikut ini.
Jika diketahui fungsi f(x), maka turunan fungsi f(x) pada x adalah:
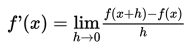
Tentu sekarang kalian sudah ingat, kan? Jika sudah, mari kita simak penjelasan berikut.
1. Turunan Fungsi Konstan
Fungsi konstan adalah fungsi dengan bentuk f(x) = n dengan n = bilangan real. Turunan fungsi konstan menggunakan limit fungsi adalah sebagai berikut.
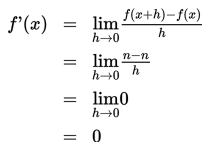
Jadi, turunan fungsi yang berbentuk nilai konstan adalah 0.
Jika diketahui f(x) = n, dengan n bilangan real, maka f '(x) = 0
2. Turunan Fungsi Identitas
Fungsi identitas adalah fungsi dengan bentuk f(x) = x. Turunan fungsi identitas menggunakan limit fungsi adalah sebagai berikut.

Jadi, turunan fungsi identitas adalah 1.
Jika diketahui f(x) adalah sebuah fungsi identitas atau f(x) = x, maka f '(x) = 1
3. Turunan Fungsi Pangkat
Misalkan diketahui fungsi pangkat dengan bentuk f(x) = xn dengan n bilangan bulat positif. Untuk menentukan rumus umumnya, kita dapat mencari pola dari hasil yang diperoleh melalui tabel berikut.
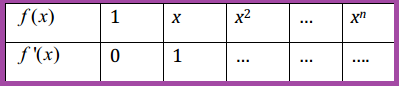
Sekarang, kita tentukan dahulu turunan fungsi untuk n = 2.
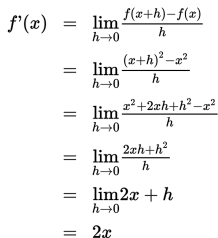
Kita masukkan hasilnya ke dalam tabel berikut ini.
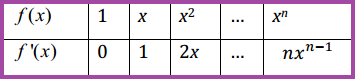
Coba kalian perhatikan tabel di atas. Dari tabel tersebut, dapat terlihat pola yang terbentuk sehingga diperoleh kesimpulan sebagai berikut.
Turunan untuk fungsi f(x) = xn adalah f '(x) = nxn-1 dan turunan untuk fungsi f(x) = mxn adalah
f '(x) = mnxn-1
f '(x) = mnxn-1
Agar kalian lebih memahami penggunaan aturan turunan fungsi di atas, mari kita perhatikan contoh berikut.
Contoh:
Tentukan f '(x) dari fungsi berikut.
a. f(x) = 6x
b. f(x) =
Penyelesaian:
a. f(x) = 6x → f '(x) = 6
b. f(x) =
f(x) = → =
4. Turunan Jumlah dan Selisih Fungsi-Fungsi
Jika diketahui fungsi y = f(x) = u(x) ± v(x) dengan turunan dari u(x) adalah u ‘(x) dan turunan dari v(x) adalah v ’(x), maka turunan dari f(x) adalah:
f '(x) = u '(x) ± v '(x)
Agar kalian lebih paham penggunaan aturan turunan fungsi aljabar di atas, mari perhatikan contoh berikut.
Contoh:
Carilah turunan fungsi g(x) = 2x2 + .
Penyelesaian:
Misalkan u (x) = 2x2 dan v(x) = , maka:
u ' (x) = 4x dan v '(x) =
Dengan demikian, turunan fungsi g(x) adalah:
g '(x) = u ' (x) + v '(x) = 4x +
5. Turunan Hasil Kali Fungsi-Fungsi
Jika diketahui fungsi y = f(x) = u(x).v(x) dengan turunan dari u(x) adalah u ‘(x) dan turunan dariv(x) adalah v ’(x), maka turunan dari f(x) adalah:
f '(x) = u ‘(x).v(x) + u(x).v ’(x)
Agar kalian lebih paham penggunaan aturan turunan fungsi aljabar di atas, mari perhatikan contoh berikut.
Contoh:
Tentukan turunan fungsi f(x) = 2x(x4 - 5).
Penyelesaian:
Misalkan u(x) = 2x dan v(x) = x4 - 5, maka:
u '(x) = 2 dan v '(x) = 4x3
Dengan demikian, diperoleh:
f '(x) = u ‘(x).v(x) + u(x).v ’(x) = 2(x4 - 5) + 2x(4x3 ) = 2x4 - 10 + 8x4 = 10x4 - 10
6. Turunan Hasil Bagi Fungsi-Fungsi
Jika diketahui fungsi y = f(x) = dengan turunan dari u(x) adalah u ‘(x) dan turunan dariv(x) adalah v ’(x), maka turunan dari f(x) adalah:
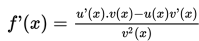
Agar kalian lebih paham penggunaan aturan turunan fungsi aljabar di atas, mari perhatikan contoh berikut.
Contoh:
Tentukan turunan fungsi .
Penyelesaian:
Misalkan u(x) = 3x4 dan v(x) = 2x - 5, maka:
u '(x) = 12x3 dan v '(x) = 2
Dengan demikian, diperoleh:
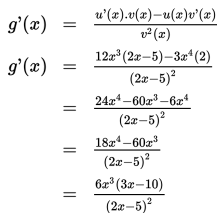
No comments:
Post a Comment